I recently had a chance to take a class called MAE195: Numerical Methods. This course was offered in 2022 by the Mechanical Engineering department at the University of California, Irvine and taught by Perry Johnson.

Basically, numerical methods are a way of approximating sometimes impossible-to-solve math problems with computers.

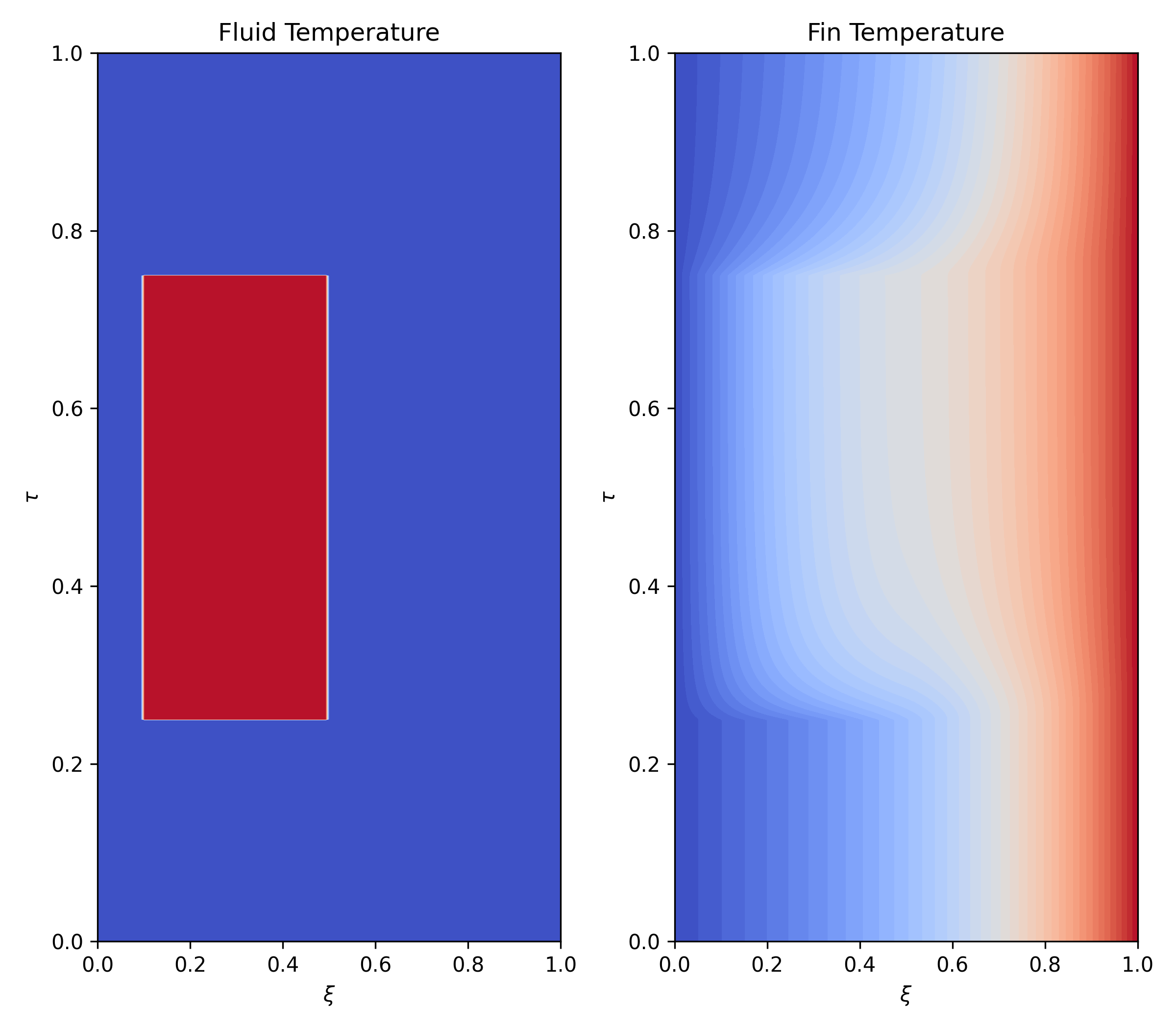
You can create cool things like this, which is a contour plot of heat across (x-axis) a 1-d fin (right) exposed to a fluid whose temperature varies with time (left), with constant temperature boundary condition. This is a solution to a time-varying (y-axis) heat equation of such a system.

I was very excited to take this course, because doing computer simulations is something I love and it allowed me to investigate some of what np.linalg actually does under the hood.

Our final project was to produce an accurate simulation of the 1-D heat equation on a fin, whose left and right sides are attached to a constant-temperature heat sink and whose body is exposed to a heated (or cooled) fluid. Then, we are tasked with determining the steady state and time dependent temperature distributions across the fin. My report turned out alright. I figured I would publish it on the internet, because: why not!

Here is the report

• misc